Geometri i svensk matematikundervisning har idag tonvikten mer på mätning än på Euklidisk konstruktionsgeometri. Det finns dock fortfarande ett visst utrymme att diskutera konstruktion av geometriska objekt och dess betydelse för matematiskt tänkande.
- Geometrins ställning diskuteras världen över. Jämfört med Lgr 80 så har kursplanen tydligare inslag av kvalitativa begrepp som t ex att känna igen, beskriva, avbilda, konstruera samt av mönster och estetiska perspektiv. Sedan gammalt är geometrin också ett område lämpligt för logiska resonemang och deduktiva studier. (Kommentar till grundskolans kursplan och betygskriterier i matematik, 1997, s 25)
Konstruktion med dator
I Sverige, där vi ersatt så gott som hela konstruktionsgeometrin med mätning, har naturligtvis datorprogram som bygger på Euklidiska konstruktioner ingen stor marknad. I USA, ett land där man fortfarande tillåter sig att erbjuda en ettårig (!) kurs i Geometri på gymnasienivå, används GSP på ett flertal high schools. Även om denna artikel kommer att exemplifiera med konstruktioner från GSP, är de två programmen så snarlika i uppbyggnad och användning att användare av Cabri-Géomètre bör kunna känna igen sig.
"Konstruktionen blir en träning i Euklidiskt tänkande."
I många avseenden är måhända GSP mer flexibelt än Cabri,
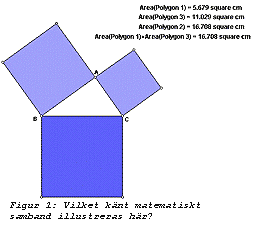
detta sagt utan att vi haft tillfälle att testa någon "äkta" Windows-version av Cabri. Exempelvis tillåter GSP att man definierar "Polygon interior" . Detta kommer väl till pass när man vill mäta exempelvis area. Med hjälp av den inbyggda kalkylatorn definierar man lätt uttryck som skall beräknas. Se figur 1.
Programmet startar med ett "anteckningsblock", där man kan rita eller konstruera geometriska objekt. Senaste versionen av GSP, version 3 för Windows och Mac, innehåller dessutom möjligheten att införa ett koordinatsystem, men det utelämnar vi i denna artikel. På anteckningsblocket kan man konstruera punkter och efter det linjer, strålar, segment, cirklar. Därefter kan man gå vidare med att konstruera punkter på objekt, mittpunkter, skärningar, etc. Konstruktionen blir därigenom också en träning i Euklidiskt tänkande. Dock får begrepp som passare och linjal en delvis ny innebörd. Att slå en cirkelbåge innebär att hela cirkeln ritas. Även avbildningsgeometriska operationer är möjliga, såsom translation, vridning och spegling.
Exempel 1: Innebörden av ett bevis
Innebörden av ett geometriskt bevis och hur det bör formuleras
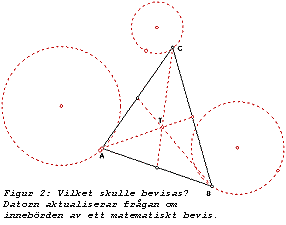sätts på sin spets. Vilka möjligheter finns att generalisera utifrån vad som kan iakttas på skärmen? Om man föreställer sig en triangel som genomlöper alla tänkbara skepnader, vilket kan göras genom att låta de tre hörnpunkterna vara punkter på tre olika cirklar som genomlöpes i olika takt, och ett visst förhållande som man definierat kvarstår, är detta då bevisat? Se figur 2.Påståendet:
Medianerna i en triangel skär varandra i en punkt T, triangelns tyngdpunkt.
är lätt att verifiera genom att låta GSP utföra en animering, dvs de tre punkterna A, B och C löper runt respektive cirkel på samma gång i en dynamisk konstruktion. Vi skulle också kunna låta GSP mäta hur T delar varje median och därigenom "bevisa" att punkten T delar varje median i förhållandet 2:1 räknat från motsvarande hörn.
Konstruktionsproblem
Såväl GSP som Cabri är "Euklidiskt stelbenta". Om man inte konstruerar objekt på rätt sätt från början, kommer man aldrig fram till en slutlig lösning. Detta är i allmänhet lätt att inse redan efter en kort stunds arbete med programmet.
Exempel 2
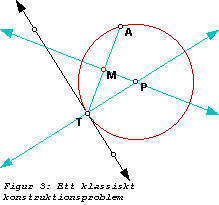
Konstruera en cirkel som går genom en given punkt A och som tangerar en given rät linje i T.
Det är lätt att konstruera en linje och en punkt T på denna. Men hur hittar man cirkeln som går genom A och tangerar linjen i T?Figur 3 illustrerar en metod, som bygger på att hitta två diametrar för att kunna bestämma cirkelns medelpunkt. Studenter som arbetar på ett problem av denna typ, kommer att upptäcka att om man känner till att mittpunktsnormalen till en korda också är diameter i en cirkel, så ger det också lösningsstrategin. Se figur 3.
Makroprogrammering eller Script
|
Lägg märke till att man måste ha två punkter definierade innan man "spelar upp" detta script. Man markerar punkterna genom att hålla nere shift-tangenten samtidigt som man klickar på respektive punkt. Detta script konstruerar en liksidig triangel med en "klassisk" metod. Punkterna A och B är två av triangelns hörn.
Resultatet av en uppspelning av detta script ser vi i figur 5. Observera att en del av konstruktionen är "dold" (hidden). Den kompletta konstruktionen kan naturligtvis synliggöras när man så önskar.
Animering och LocusAtt spåra ett "locus", dvs en punkt eller ett objekt som rör sig under en animering kan vara mycket illustrativt, speciellt eftersom GSP tillåter stor frihet i att färglägga objekt, göra linjer eller cirklar tjocka, tunna eller streckade
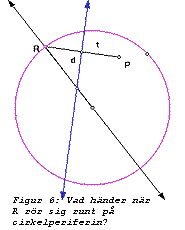
I figur 6 visas en till synes enkel konstruktion,
bestående av en cirkel, en punkt P inuti cirkeln som är sammanbunden med diametern vid R, via ett segment t, som delas mitt itu av en mittpunktsnormal vid d. Om vi nu "spårar" denna mittpunktsnormal när R rör sig varvet runt utefter cirkelns periferi, vilken typ av figur får vi då? Vad händer om vi flyttar ut punkten P utanför cirkeln? En undersökning som denna kan användas om vi vill utreda sambandet mellan hyperbel, ellips och parabel. Resultatet framgår av figur 7.Användbarhet och konsekvenser i en undervisningssituation
Vi anser att användning av ett datorprogram som The Geometer´s Sketchpad ger möjlighet att kommunicera ett geometriinnehåll på ett kvalitativt nytt och annorlunda sätt. Särskilt gäller detta situationer när man tar del av en konstruktions uppbyggnad. Detta kan i programmet ske i en dynamisk framställning. Dessutom kan tillvägagångssättet göras tydligt för andra än konstruktören själv. Här är scriptfunktionen av avgörande betydelse.
Arbetet med att finna lösningar på ett givet geometriskt problem sker med fördel i par eller grupp, vilket ger förutsättningar för en dialog kring den framväxande lösningen. Med utnyttjandet av olika teknik för att föra utförda konstruktionsuppgifter vidare, bifogade dokument på e-mail, diskett etc kan lösningar arbetas fram i kommunikation mellan student och student och/eller mellan student och lärare.
Möjligen kan en viss fara ses i att den geometriskt oerfarne användaren helt litar till det som iakttas på skärmen dvs generaliseringar görs utifrån en eller ett fåtal situationer. Den studerande litar till att datorprogrammet i sig utgör en garanti för att ett visst geometriskt påstående är sant.
Vår erfarenhet som lärarutbildare är att många blivande matematiklärare inte bara låter sig fascineras av dynamiken och möjligheterna i GSP utan också börjar fundera kring sitt eget förhållningssätt till ämnet. Vad är egentligen ett bevis? Är det mitt eget kunnande eller datorprogrammet i sig som står för det matematiskt korrekta?
Ett annat faktum är att användandet av GSP lyfter fram skiljelinjen mellan att rita och konstruera. Ett arbetsmaterial med exempel som tydliggör denna skillnad stimulerar till ytterligare diskussioner.
Inom lärarutbildningen vid Göteborgs universitet har vi låtit studenterna jämföra sina lösningsstrategier vid papper och penna konstruktioner med motsvarande konstruktioner i GSP.
Vi avslutar med ett problem, se nästa sida. Resultaten av en undersökning inbegripande detta problem kommer bl a att redovisas vid Matematikbiennalen i Sundsvall, januari 1998.
Referenser
Key Curriculum Press. (1995). The Geometer’s Sketchpad. Berkeley, Kalifornien, USA.
Skolverket (1997). Kommentar till grundskolans kursplan och betygskriterier i matematik. Stockholm: Liber distribution.
Lingefjärd, T & Holmquist, M. (1997). Arbetsformer, arbetssätt och examination i en
|
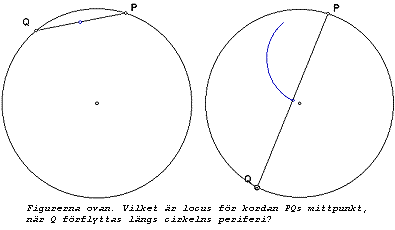
DiU inbjuder: Lös problem! På en godtycklig cirkels periferi finns en fix punkt P. På samma cirkels periferi finns en godtycklig punkt Q, skild från punkten P. Punkterna sammanbinds med ett linjesegment, en korda. a) Undersök läget hos kordans mittpunkt för olika placeringar av punkten Q på cirkelperiferin. Utför dina konstruktioner på papper med penna, passare och linjal. Hur motiverar du dina slutsatser? b) Undersök läget hos kordans mittpunkt för olika placeringar av punkten Q på cirkelperiferin. (precis som i uppgift a!). Utför dina konstruktioner i datorprogrammet The Geometer's Sketchpad (GSP). Hur motiverar du dina slutsatser? c) Redogör för likheter och skillnader i ditt sätt att genomföra och ta fram argument för lösningen av uppgift a och b. Sänd in lösning! Vi inbjuder läsarna att själva eller tillsammans med elever undersöka detta problem. Skriv till Datorn i Utbildningen,redaktionen, FFörridargrändouml;rridargrFörridargrändauml;nd 16, 165 52 H165 52 Hässelbyauml;sselby. De tre bästa bidragen insända före den 12 januari belönas med priser. Resultaten av en undersökning inbegripande detta problem kommer även att redovisas vid Matematikbiennalen i Sundsvall, januari 1998. Thomas Lingefjärd & Mikael Holmquist |
Institutionen för Ämnesdidaktik,
Göteborgs Universitet
Box 1010, 431 26 Mölndal
tel 031-773 22 53
fax 031-773 22 81
mobil 0708-29 39 73
e-post: thomas.Lingefjard@ped.gu.se
webb: didserv.did.gu.se/matemati/thomas.htm
|
Matematik-
biennal 1998 Under rubriken "Matematik som kultur" hålls Matematikbiennalen i Sundsvall, 21-23 januari 1998. Biennalerna är ett led i arbetet med att förbättra svensk matematikundervisning genom att uppmärksamma och sprida goda idéer, kunskap och erfarenheter från utvecklingsarbete och forskning om matematikämnets mål, innehåll och om undervisning och inlärning i matematik. Utlovas en härlig matematikfest med lagom proportioner av nostalgi, visioner, forskningsrön, utställningar och spännande möten. Aktuella områden inom matematik i förskola, grundskola, gymnasium och vuxenutbildning belyses. De gångna matematikåren belyses med sedvanlig humoristisk snärt, av Jan Unenge och hans revyensemble. Pris för deltagande i hela konferensen är 3 400 exkl moms. Anmälan till Kongressbyrån Sundsvall, tel 060/55 00 20, Box 890, 851 24 Sundsvall, e-post: zarih.nordin@kongressbyranis-vall.se, webb-adress: www.mh.se/publik/mabi. |
Åter till DiUs indexsida